The Singularity is not coming
On the speed of progress
2012/08/10
Note from the future: this 2018 article by P. Collison and M. Nielsen now provides data to back up this hypothesis. What follows is from 2012.
If you are tech-savvy, by that point you have almost certainly come across the idea of the Singularity [1] as defended by futurists like Ray Kurzweil and Vernor Vinge. As a reminder, it is the notion that, when we are at last able to compile a smarter-than-human artificial intelligence, this AI will in turn manage to improve its own design, and so on, resulting in an out-of control loop of "intelligence explosion" [2] with unpredictable technological consequences. (Singularists go on to predict that after this happens we will merge with machines, live forever, upload our minds into computers, etc.)
What's more, this seemingly far-future revolution would happen within just a few decades (2040 is often mentioned, though it's getting pushed back every now and then), due to the "exponential" rate of progress of science. That this deadline would arrive just in time to save the proponents of the Singularity from old age is just a weird coincidence that ought to be ignored.
As a scientist, I find the claim that scientific progress is exponential to be extremely dubious. If I look at my own field, or at any field that I am vaguely familiar with, I observe roughly linear progress, at a rate that has typically been going on since as far back as the field's foundation. Exponential progress claims are usually supported by the most bogus metrics, such as the number of US patents filled per year [3] (which is a measure of the number of people employed in a field, not a measure of the speed of its progress).
And as somebody who does AI research, I find the notion of "intelligence explosion" to make no sense, for reasons reaching back to the very definition of intelligence. But I am not going to argue about that right now, as isn't even necessary to invalidate the notion of the Singularity.
“ A hypothetical self-improving AI would see its own intelligence stagnate soon enough, rather than explode
I would like to simply argue that scientific progress is in fact linear, and this despite the capitalization of past results into current research ("accelerating returns"), and despite an exponentially increasing population of scientists and engineers working on advancing it (resource explosion). And since I don't want to argue in the realm of opinion, I am going to propose a simple, convincing mathematical model of the progress of science. Using the same model, I'll point out that a hypothetical self-improving AI would actually see its own research progress and intelligence stagnate soon enough, rather than explode –unless we provide it with exponentially increasing computing resources, in which case it may do linear progress (or even better, given a fast enough exponential rate of resource increase).
The problem of progress
The resources that we devote to science have been exploding throughout history. The world population of scientists has been doubling roughly every 50 years from 1500 to 1900 [4], and has kept an exponential rate throughout the 20th century as well, by what seems to be a factor of 10 every 50 years [5] (it is however unclear whether that growth is still being sustained now [5], and even if still exponential the rate has evidently gotten slower). Likewise, the number of papers and patents has followed exponential growth during the past century, unsurprisingly since average paper count per scientist is unlikely to change significantly.
Besides available researcher brains, the computing resources available to science have followed exponential growth as well (Moore's law) in the past 50 years.
Furthermore, each new scientific discovery accelerates the pace of science to some extent, because it gives future researcher a better understanding of the field considered, as well as new tools to work with. That's "accelerating returns". You get to stand on the shoulders of giants.
And yet despite all this, if you look at the actual understanding of the world that we have achieved, if you look at real *impact* rather mere volume, the general impression you get is that scientific progress has really been linear. We didn't "get" physics 50 times better in 1990 compared to 1940. The 1940-1990 progress of physics might even have been slightly less significant than the 1890-1940 one, actually.
Even in a new, ultra-fast growing field such as computer science, most of the state of the art algorithms currently around date back from the 60s and 70s. Our computers may be 10^6 faster now than in 1960, but our knowledge is only a few times broader, our algorithm libraries only a few times better. Likewise neuroscience and AI have followed slow, noticeably linear growth since the 50s.
So how do we explain that huge dichotomy between exponential resource growth and perceived linear progress? What's happening?
Well, a widely-noticed empirical fact about science is that within a given field, making an impact is getting exponentially more difficult over time. Just look: the big discoveries in quantum physics had all been reaped by 1930. Most of what could be said in Newtonian physics had been said by Newton himself. Information Theory researchers will never surpass in impact the single 1948 paper that founded their field, no matter how long and fruitful their career. The list could go on.
In fact, the only way you could hope to really matter in science these days is by founding a new field or subfield –by augmenting a research axiom to the point that it frees new potential big discoveries. Imagination trumps intelligence and hard work every time.
The reason is simply that founders and first comers reap all of the high-impact low-hanging fruit, and thus after each major discovery, the amount of effort to reach the next one gets multiplied by a certain factor. By the time you join a field where 10,000 people have already spent their career, your impact expectation will be low, and your thesis title seriously obscure.
Let's come up with a trivial model and see if increase in discovery difficulty really is *exponential* (or inversely, that at equal difficulty, discovery impact is getting exponentially lower –both are strictly equivalent). If you're already convinced, skip to the next part!
Science gets exponentially harder
Let's consider a finite set of potential discoveries D within a new scientific field (let's say 100 discoveries). Each potential finding has an "impact" value following a random uniform distribution between two extrema (let's say, a random integer between 0 and 100), and an "effort necessary for discovery" also following a random uniform distribution (let's go again for 0-100). The values I'm mentioning are unimportant and are there to allow you to visualize the problem, dear reader, the only meaningful thing is that I chose random uniform distributions in both cases, which I do because I have no data. Anything else than pure randomness would be too wild a guess.
Now let's have a population of researchers that each have an equal number of "effort points" to spend on discoveries over their careers, let's say 100 points. They come in succession, and each researcher tries to maximize the total impact she can make within the effort she can spend. The sum of the effort factors of the discoveries they make must be smaller or equal to their total effort points. Of course, discoveries can't be made twice.
Well what have we there, if not an iterated Knapsack problem! Let's try to run that in Matlab a few times with different random initial distributions, and let's average the results. Why yes I love Matlab.
Here's what I get after averaging 100 trials.
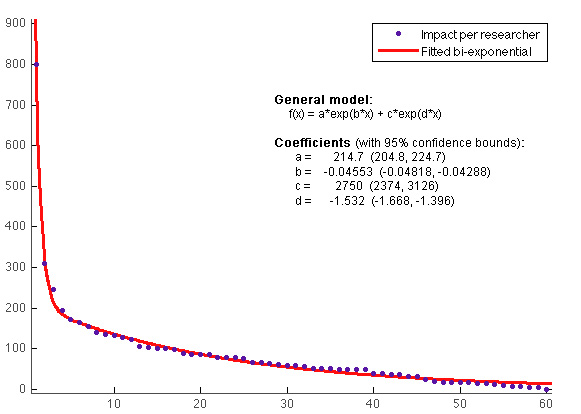
Exponential decrease of discovery impact of each succeeding researcher. The first researcher to the field makes on average a 801 "impact points" contribution to the field, the second 310, the third 246, etc.
And it doesn't really matter how many discoveries are available, one hundred or one million, or how much effort researchers are spending, since these parameters only change the scale of evolution of the graph (as long as both are finite –infinite available discoveries would be a different stories, you'd have progress proportional to effort).
Conclusion so far: scientific progress in a given field gets exponentially harder, as widely empirically noticed. Of course paper count per researcher will stay about constant despite this (or patent count, though that one tends to increase by fashion). Mostly, what happens is that papers get increasingly narrow and obscure as the field age, also an empirically obvious trend.
Essentially that's why scientific progress is linear within a given field: accelerating returns and exponential growth of scientific resources are merely *compensating* for the increasing difficulty of doing science that matters, the two canceling each other out into linear growth.
As a side-note: in real life, scientific fields (and thus potential discovery pools) are not set in stone, to the contrary the axioms they are built on regularly evolve, freeing new potential important discoveries for that field (or sprouting new subfields, possibly even entirely new fields, like, say, computer science). It would be enough to invalidate the simple model I'm proposing, and I tackle the objection in the last part of this article.
Now onward with another simple model for a self-improving AI.
The case of the self-improving AI
Let's have a hypothetical AI that researches artificial intelligence, and that constantly rewrites its own code to incorporate its finding into its own intelligence. I guess it's an AI that doesn't have much regard for its own past identity, or at least that considers its quest to be more important. It would probably feel weird to rewrite your own source code, hey, gives me an idea for an associated reward system. Anyway.
Its first discovery takes ΔT of time, and results in an "amount of knowledge" (or "impact") K that allows a speedup of the time its takes to make the next discovery (at equal "discovery effort" spent). Next discovery would take ΔT/(ft.K). That is to say thats at equal impact, discovery time would be an exponentially decreasing series of factor ft > 1 (the "intelligence explosion" scenario).
Also, we model discovery impact (at equal effort spent) as an exponentially decreasing series, as validated by our little model above. Of factor fi > 1.
So after the N-1th discovery, our AI has made a total impact of:
for N big enough, and and the Nth discovery is done in ~ ΔT/(C.ft). Of value K/(fi^N). So at that point its progress rate is:
Conclusion: the rate of progress of the AI converges exponentially toward 0, like that of a frustrated grad student. (As a side-note, if you give to the AI exponentially increasing resources (of factor fr), it can manage a linear rate of progress if fr~fi, much like what happens with scientific progress at large.) Then again, this is an asymptotic behavior, so if the number of available "big" discoveries is large enough, you could observe a locally exponential progress rate at the start of the curve. On the long term, though, progress rate *will* decreases exponentially.
Seems pretty intuitive actually, if you admit that there is only so much that one can discover about intelligence.
Paradigm shifts and imagination
As I pointed out earlier, in real life the paradigms on which scientific fields get founded tend to evolve over time, which means that the set of available discoveries that researchers can "chose from" will tend to expand over time. Paradigm shifts increase the scope of research that can be done. For instance, inventing transistors opened up the entirely new field of what to do with them. Or coming up with the basics of quantum physics. And so on.
I'd like to argue that these paradigm shifts can be modeled using the exact same model that I used for discovery. We start with a finite pool of possible paradigm shifts, we devote exponentially increasing resources to finding them ("resources" meaning "researchers", since each researcher tries a little to find out-of-the box ideas), and what happens is that 1) shift volume explodes over time, like papers published did earlier, because they're a linear function of resources, and 2), the real impact at large of each shift decreases exponentially. Resulting in a linear growth of shift impact; which means in turn that the pool of available potential scientific discoveries increases merely linearly. Here's a graph to illustrate the idea, the graph of linear scientific progress at a larger scale (we don't picture individual paradigm shifts, instead we abstract them into shifts of equal cumulated impact, that happen at a linear rate):
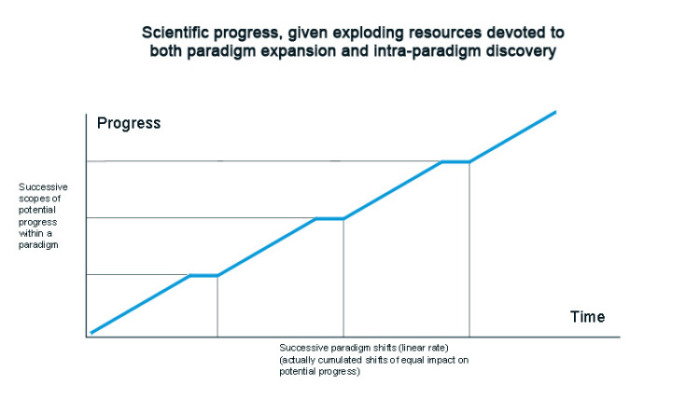
Within each potential progress scope freed by a paradigm shift, progress is linear given exponential resources. Scope expansion are linear as well, given exponential resources.
So what to make of this?
- Science advances linearly given exploding resources, and thus its pace will slow down in the future as the resources that we devote to it dwindle. Keep that in mind.
- Also, a piece of advice: as a researcher, you've got to work at the 2nd level of discovery, the paradigm level, because it's so much more impact-efficient. Don't devote your energy to discovering tiny new things within the old paradigm you inherited from your thesis advisor, rather discover broad news ideas entirely. Be imaginative.
Intelligence is just a skill, more precisely a meta-skill that defines your ability to gain new skills. But imagination is a superpower. Do not rely solely on your intelligence and hard work to make an impact on this world, or even luck, it's not going to work. After all the total quantity of intelligence and hard work available around is millionfold what you can provide –you're just a drop of water in the ocean. Rather use your imagination, the one thing that makes you a beautiful unique snowflake. Intelligence and hard work should be merely at the service of our imagination. Think outside of the box. Break out. Shake the axioms.
“ The total quantity of intelligence and hard work available around you is millionfolds what you can provide –you're just a drop of water in the ocean
And as a side-note, Ray Kurzweil does not get talked about because of his research, but because he used his wild imagination to come up with far-fetched visions of the future : )
Now of course one would need to go out there and gather invalidating or validating data for the mathematical model I presented. But this is not a paper and I don't have time for this. Take my model for what it's worth: as something you've read on a random blog.
References
[1] What is the Singularity? - The Singularity Institute
[2] Intelligence explosion: evidence and import - Luke Muehlhauser, Anna Salamon
[3] Accelerating change - Wikipedia
[4] The historical demography of the scientific community, 1450-1900 - Robert Gascoigne
[5] The Big Crunch - David Goodstein